Chance and Probability

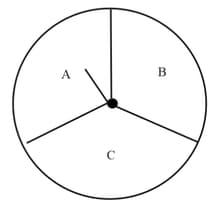
Suppose you spin the wheel, find the probability of not getting a green sector

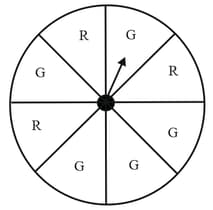
Suppose you spin the wheel, find the probability of getting a green sector

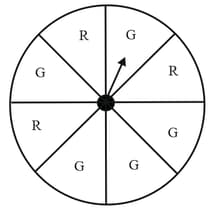
Suppose you spin the wheel, list the number of outcomes of getting a green sector and not getting a green sector on this wheel

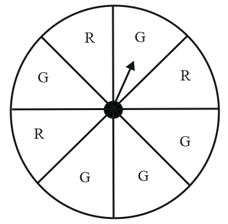
You have a bag with five identical balls of different colours and you are to pull out (draw) a ball without looking at it; list the outcomes you would get.

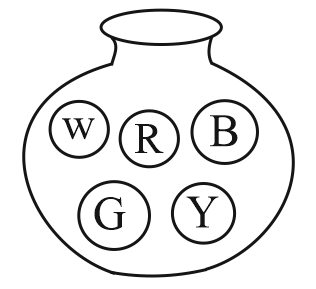
When you spin the wheel shown, what are the possible outcomes? List them.

When a die is thrown, what are the six possible outcomes?

If you try to start a scooter, what are the possible outcomes?

When a die is thrown, what are the six possible outcomes?

If you try to start a scooter, what are the possible outcomes?

A dice is thrown once. Find the probability(in fraction) of getting an odd number.

If $n\left(A\right)=2, p\left(A\right)=\frac{1}{5}$, then $n\left(S\right)=$

Two players, $A$ and $B$, play a chess match. It is given that probability of $A$ winning the match is $\frac{5}{6}$. Find the probability of $B$ winning the match.

If $n\left(A\right)=2, P\left(A\right)=\frac{1}{5}$, then $n\left(S\right)=$?

In a throw of a die, find the probability of getting a number less than $4$.

A dice is rolled. What is the probability that the number appearing on its upper face is less than $3$?

Which number cannot represent a probability ?

A card is drawn at random from a pack of well shuffled $52$ playing cards. Find the probability that the card drawn is -

(1) an ace. (2) a spade.

A two-digit number is formed with digits $2,3,5,7,9$ without repetition. What is the probability that the number formed is

(1) an odd number ?

(2) a multiple of $5$ ?

There are $15$ tickets in a box, each bearing one of the numbers from $1$ to $15$. One ticket is drawn at random from the box. Find the probability of event that the ticket drawn -

(1) shows an even number.

(2) shows a number which is a multiple of $5$.

If two dice are rolled simultaneously, find the probability of the following events.

(1) The sum of the digits on the upper faces is at least $10$.

(2) The sum of the digits on the upper faces is $33$.

(3) The digit on the first die is greater than the digit on second die.